Basic Roofline Model
Roofline model is used to analyze the performance bottleneck of a program running on a specific hardware. It’s sustainable performance is bound by:
where AI means Arithmetic Intensity, the ratio of floating operation and memory access, which is determined by the application / algorithm itself.
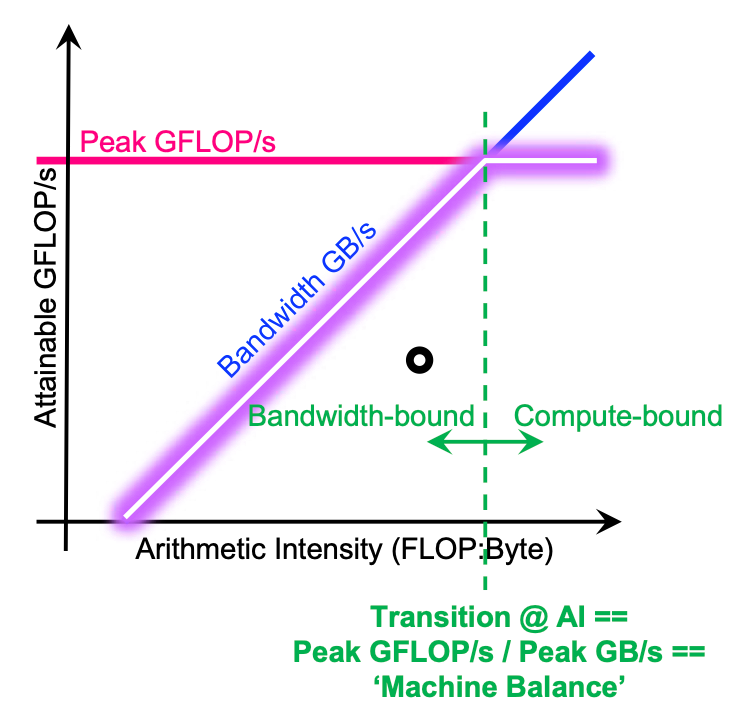As the figure1 shows above, when AI of the application locates in the ramp part of roofline diagram, the performance is bound by memory bandwidth. It induces that the number of floating point operation performed on each accessed byte is small, and the performance could be boosted by increasing the number of floating point operations, i.e., increase AI and move right. We call these application memory-bound, which have poor locality (data reuse) and demand large amount of data while computing. When AI sits in the plain part of roofline diagram, it means that the performance is bound by the theoretical performance of the specific hardware. In this scenario, increasing AI is helpless since the processors are tired of processing the incoming data. This kind of applications are compute-bound.
Note that the slope () of the ramp part is the bandwidth of memory (DRAM):
And the turning point of diagram represents the “machine balance” point, i.e., the minimum arithmetic intensity needed to reach the peak floating point performance. It can be computed via theoretical GFLOP/s and memory bandwidth.
Roofline Considering Hierarchical Memory
When combining multiple hierarchies of memory, the roofline diagram could tell you about the cache locality.
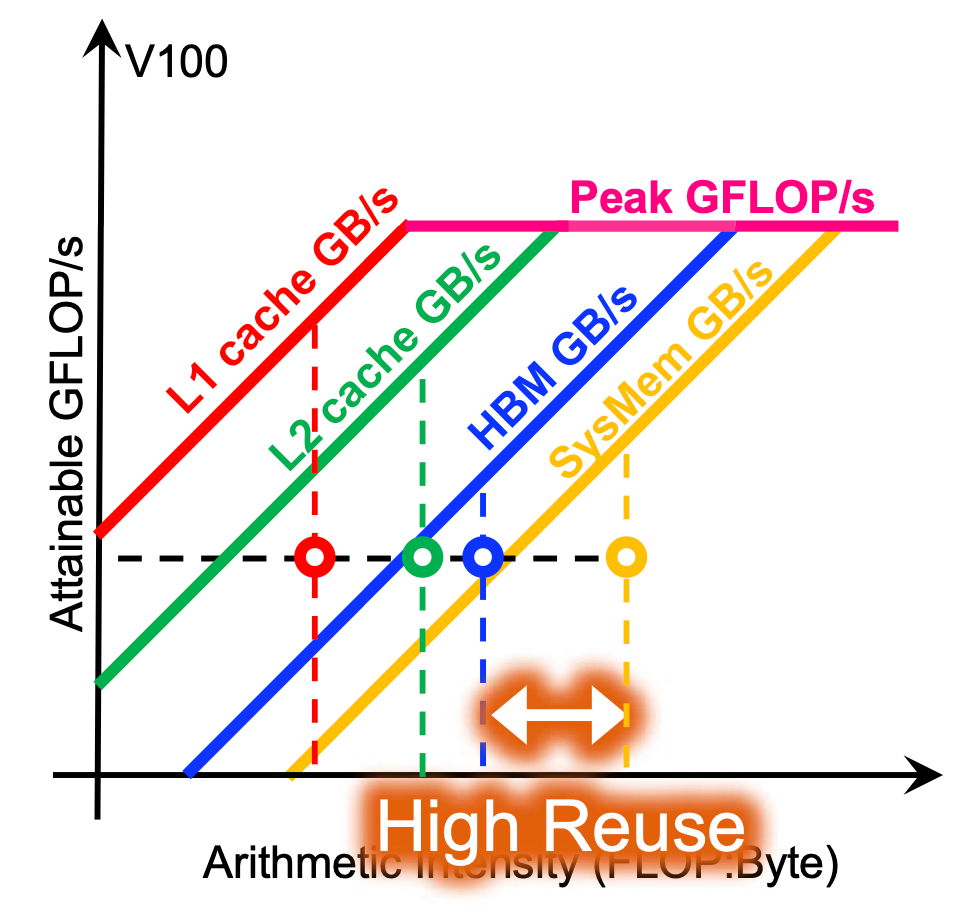The figure above demonstrates roofline model diagrams of different memory hierarchies. What we can obtain is faster cache usually comes along with lefter turning point. It means that achieving peak performance needs less arithmetic intensity. The closer turning point to the left, the higher bandwidth the corresponding memory has.
Roofline Guided Optimization
There are 3 possible approaches to optimize an application guided by roofline model:
Increase Parallelism
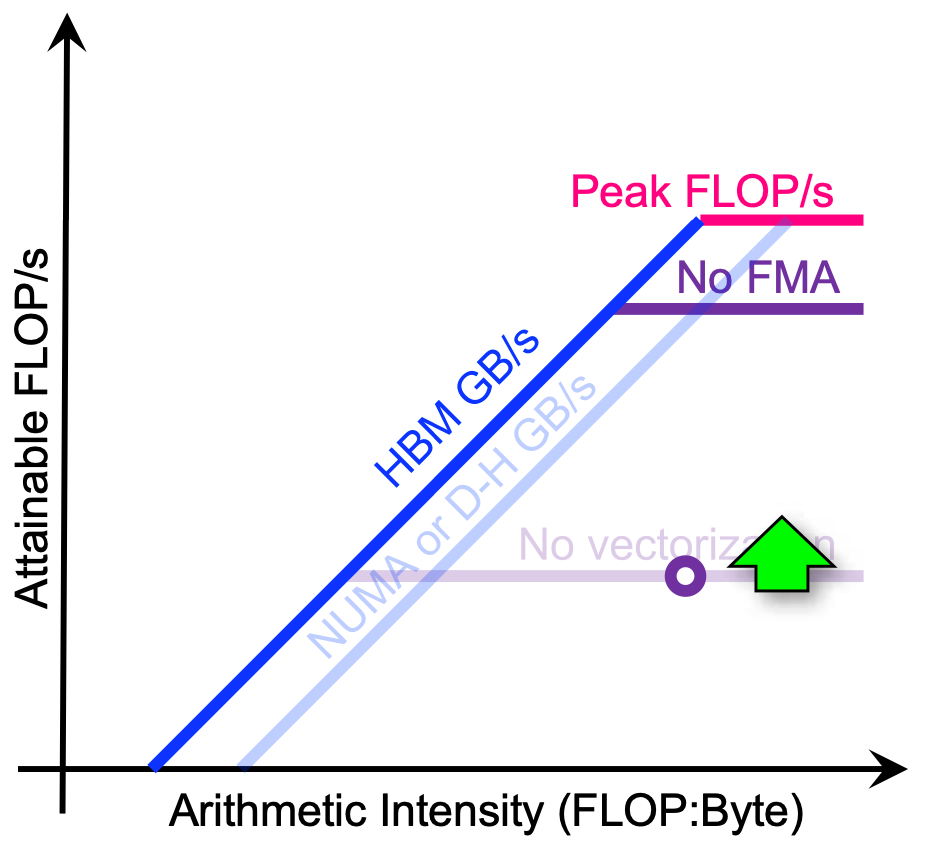
- multithreading
- vectorization
- increase SM occupancy
- utilize FMA instructions
- minimize thread divergence These methods increase the attainable FLOP/s by leveraging more computing units / cores without changing the application’s arithmetic intensity.
Maximize Memory Bandwidth
- utilize higher level caches
- NUMA-aware allocation
- avoid H-D transfers
- avoid uncoalesced memory access
Improve Arithmetic Intensity
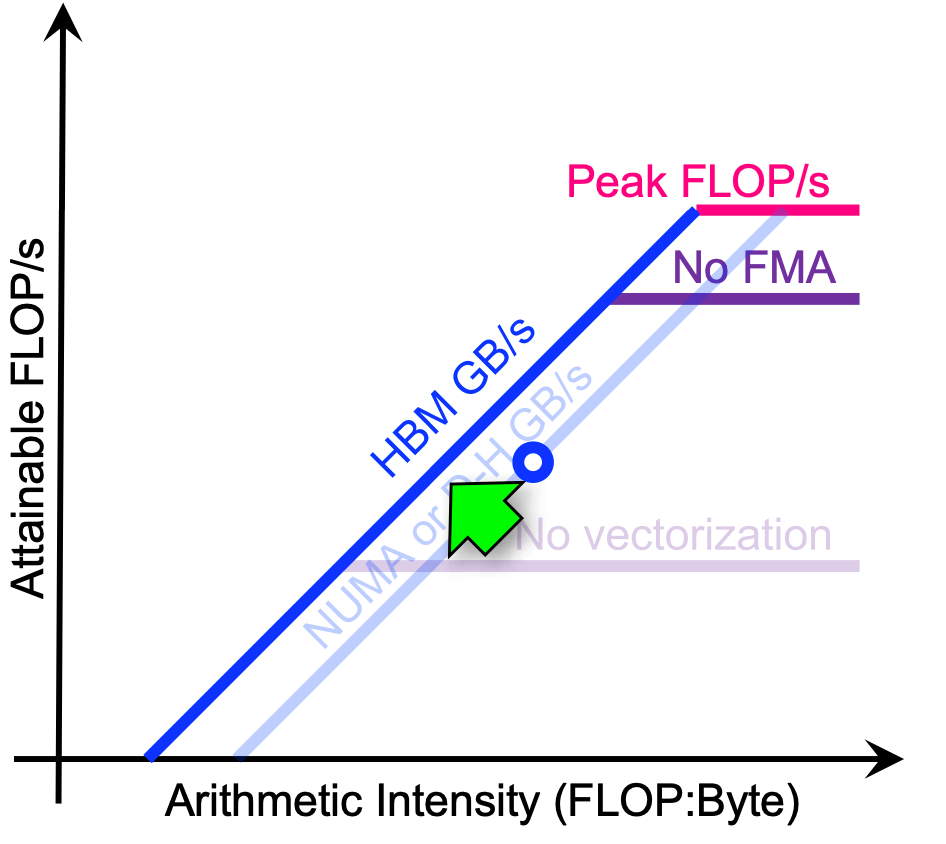
- minimize data movement
- exploit cache reuse
These methods need to modify the application to reduce memory access to slow memory hierarchy (DRAM for CPU or global memory for GPU) and keep highly reused data persisting in fast (on-chip) cache, like shared memory.
Example: NVIDIA cuBLAS
The slides give us an example about the relationships between latency and throughput, as well as the balance between ILP and TLP. See more details and discussions inside it.